Autorka: dr Aleksandra Rutkowska, Uniwersytet Ekonomiczny w Poznaniu
Potocznie mówimy o inwestorach, że grają na giełdzie, ale zastanówmy się przez moment, czy inwestowanie to rzeczywiście gra zgodnie z definicją płynącą z teorii gier1.
Gra, czyli co? Brydż, szachy czy giełda?
Nazwa „teoria gier” bywa myląca, gdyż może kojarzyć tę dziedzinę z grami komputerowymi, planszowymi, szachami lub brydżem. A faktycznie podstawową dziedziną wykorzystującą teorię gier jest ekonomia, ponieważ teoria ta zajmuje się analizą sytuacji decyzyjnych. Są to takie sytuacje, w których:
– występuje kilka osób (graczy),
– każdy z nich ma określony zbiór działań, które może podjąć w konkretnej sytuacji,
– po zakończeniu każdy z graczy otrzymuje pewną nagrodę lub karę (wypłatę),
– wypłata każdego z graczy zależy nie tylko od jego działań, ale też od działań pozostałych osób.
Najistotniejszy jest ostatni punkt. Gdyby wypłata każdej osoby zależała tylko od jej własnych działań, decyzję można podejmować na podstawie np. metod optymalizacyjnych. Przykładem takiego działania jest optymalizacja stopy zwrotu z portfela akcji2. W przypadku sytuacji strategicznej gracz rozważa też możliwe działania pozostałych graczy.
Ze względu na charakter wypłat gry możemy podzielić je na te o sumie zerowej i niezerowej. Z grami o sumie zerowej mamy do czynienia wszędzie tam, gdzie interesy graczy są dokładnie przeciwstawne, czyli zysk jednego gracza jest równy przegranej drugiego. Gry tego typu służą do modelowania sytuacji czystego konfliktu, a więc przypadków, w których nie ma mowy o współpracy między graczami.
Instrumenty pochodne jako przykład gry o sumie zero
Przykładem gry na giełdzie jest inwestycja w instrumenty pochodne. Instrument pochodny jest to taki instrument finansowy, którego wartość zależy od wartości innego instrumentu finansowego zwanego instrumentem podstawowym (bazowym). Można spojrzeć na instrument pochodny jako na rodzaj zakładu. Kupujący zakłada wzrost instrumentu bazowego w przyszłości, sprzedający – spadek. Wartość kontraktu zależy więc od instrumentu bazowego, a zarobek od trafności przewidywań, wypłata jednej strony jest stratą drugiej.
Każdy instrument pochodny ma charakter kontraktu między dwoma stronami. Ze względu na relację, jaka występuje między tymi stronami, wyróżniamy instrumenty „symetryczne”, w których obie strony przyjmują zobowiązania (kontrakty terminowe, kontrakty swap) oraz instrumenty „asymetryczne” (opcje), w których jedna strona nabywa prawo, a druga przyjmuje zobowiązanie. W przypadku pierwszych jest to zobowiązanie dwóch stron do zrealizowania transakcji kupna-sprzedaży pewnej ilości instrumentu podstawowego po określonej cenie w ustalonym terminie. W przypadku drugich opcja kupna jest to prawo zakupu określonej ilości instrumentu podstawowego (bazowego) po ustalonej cenie w określonym terminie. Natomiast opcja sprzedaży jest to prawo sprzedaży określonej ilości instrumentu podstawowego (bazowego) po ustalonej cenie w określonym terminie. Nabywający opcję uzyskuje prawo wykonania, a więc może, ale nie musi, wykonać opcję (exercising) po cenie wykonania (strike price). Schemat wypłaty opcyjnej przedstawia rysunek nr 1.
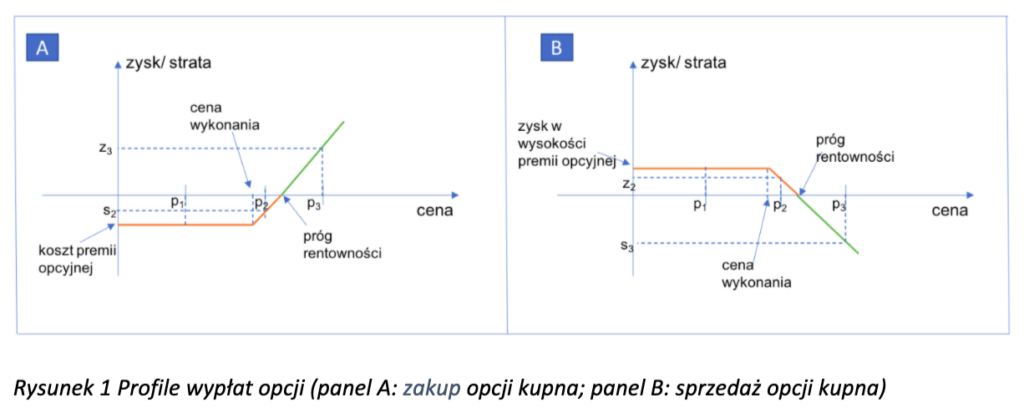
Nabywca opcji w związku z posiadanym prawem wykona opcje wtedy i tylko wtedy, gdy na rynku zajdą korzystne dla niego warunki. Przyjrzyjmy się bliżej opcji kupna (panel A, rysunek 1). Nabywca wykona opcje, gdy cena instrumentu bazowego będzie wyższa niż cena zawarta w kontrakcie będąca ceną wykonania. Należy jednak zauważyć, że wykonanie opcji przez nabywcę nie jest jednoznaczne z osiągnięciem przez niego zysku, powodem tego jest fakt konieczności zapłacenia przez nabywcę premii opcyjnej. Strata (kolor pomarańczowy linii wykresu) przechodzi w zysk (kolor zielony) w punkcie, nazywanym progiem rentowności. Próg rentowności to wartość równa cenie wykonania powiększonej o premię opcyjną. Maksymalna strata w przypadku zakupu opcji kupna równa jest wysokości zapłaconej premii opcyjnej natomiast maksymalny zysk jest teoretycznie nieograniczony. W przypadku sprzedaży opcji kupna (panel B, rysunek 1) mówimy o wystawcy opcji. Wystawca opcji osiągnie zysk w przypadku, gdy cena instrumentu bazowego spadnie a jego maksymalny zysk równy jest zapłaconej przez nabywcę premii opcyjnej.
Podstawową korzyścią ze stosowania instrumentów pochodnych jest to, iż zabezpieczają one przed niekorzystnymi dla inwestora zmianami cen instrumentów. Inną ważną korzyścią jest to, że mogą przynosić stosunkowo wysokie dochody z inwestycji, a ograniczyć straty do poziomu premii opcyjnej. Spróbujmy zatem rozważyć macierze wypłat dla opcji kupna:
– gracz A: kupuje opcje kupna (rysunek1 panel A)
– gracz B: sprzedaje opcje kupna (rysunek1 panel B)
W przypadku ceny p1 poniżej ceny wykonania, wypłaty prezentują się następująco: gracz A nie wykonuje opcji, a więc traci wysokość premii opcyjnej zapłaconej za opcję, gracz B zyskuje premię opcyjną. W przypadku ceny p2 wyżej ceny wykonania a poniżej progu rentowności; gracz A wykona opcję i zmniejszy stratę z poziomu ceny opcyjnej o różnicę pomiędzy ceną wykonania a ceną p2, a więc do wysokości s2. Zysk gracza B jest równy co do wartości bezwzględnej stracie gracza A (wartość z2). W przypadku ceny p3 powyżej progu rentowności gracz A zyskuje różnicę pomiędzy ceną p3 a progiem rentowności: z3, a gracz B traci dokładnie tyle samo, czyli s3. Zatem jest to przypadek gry o sumie zerowej.
Gdzie w tym wszystkim jest Dark Pool?
Spójrzmy na przykład liczbowy działania giełdy Dark Pool: użytkownik składa zlecenie sprzedaży 1 BTC za 40 000 USDT w ciągu 7 dni, otrzymuje za to pewną wartość w tokenach DPX. Aktualna cena BTC wynosi 38 000 USDT. Jeśli po 7 dniach cena BTC wynosi powyżej 40 000 USD, np. 42 000 USD, Dark Pool zatrzymuje 1 BTC użytkownika i przekazuje mu 40 000 USD, w przypadku ceny 42 000 USD po rozliczeniu transakcji Dark Pool osiąga zysk 2 000 USD. W przypadku ceny niższej niż 40000 USD użytkownikowi zwracany jest 1 BTC, a jedyny koszt ponoszony przez giełdę to tokeny DPX wypłacone użytkownikowi. Formalnie przyjmując zlecenie, Dark Pool kupuje opcję sprzedaży 1 BTC.
Drugim typem zleceń przyjmowanym przez Dark Pool jest zakup opcji kupna na kryptowalutę. Użytkownik składa zlecenie kupna 1 BTC za 38 000 USDT w ciągu 7 dni i otrzymuje za to pewną wartość w tokenach DPX. Jeśli po 7 dniach cena BTC wynosi poniżej 38 000 USD, np. 35 000 USD, Dark Pool przekazuje użytkownikowi 1 BTC i pobiera za to 38 000 USD. W przypadku ceny 35 000 USD po rozliczeniu transakcji Dark Pool osiąga zysk 3 000 USD. W przypadku ceny wyższej niż 38 000 USD użytkownik nie otrzyma 1 BTC, a jedyny ponoszony koszt przez Dark Pool to tokeny DPX wypłacone użytkownikowi.
W obu przypadkach pojedyncza transakcja jest grą o sumie zero. Jednak spójrzmy przez chwilę na sytuację Dark Poola, rozważając obrót całej giełdy.
Dark Pool jest w obu powyższych przypadkach kupującym opcje i za te opcje płaci w tokenach DPX. Jest ich emitentem, nie stanowią one więc dla giełdy kosztu w sensie księgowym. Odchodzi tym samym od założeń gry o sumie zero.
Przy założeniu odpowiednio dużego obrotu Dark Pool, kupując opcje kupna (gdy klient złoży zlecenie sprzedaży) i sprzedaży (gdy klient złoży zlecenie kupna) w tym samym czasie na te same aktywa, zbliża się do pozycji długiego stelaża bazującej na wzroście zmienności.
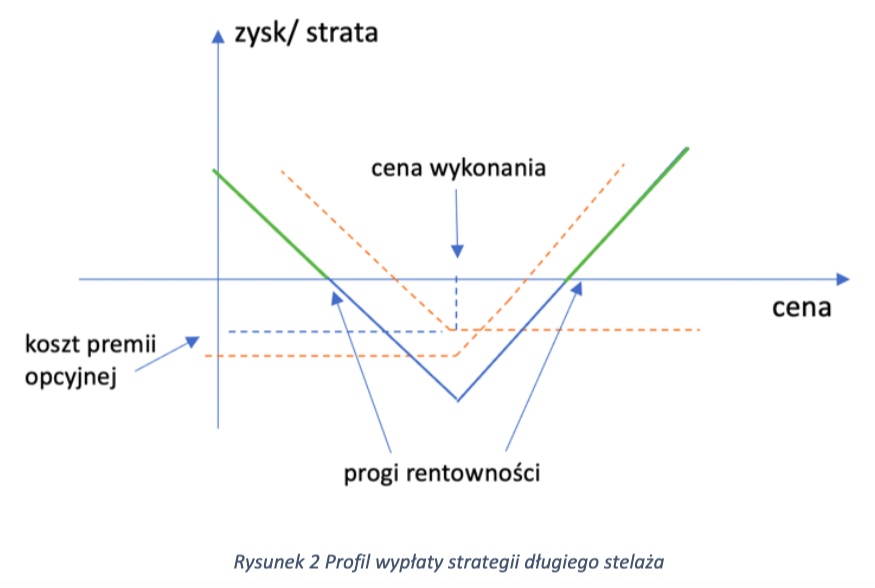
Pozycja długiego stelaża (por. rys. 2) charakteryzuje się tym, że ma nieograniczony zysk i ograniczone ryzyko, a polega na zajęciu długiej pozycji w opcji kupna i sprzedaży z założeniem, że cena wykonania obu opcji jest taka sama. Jeśli cena aktywów bazowych rośnie, potencjalna korzyść jest nieograniczona. Jeśli cena aktywów bazowych idzie do zera, zysk będzie ceną wykonania minus premie zapłacone za opcje. Maksymalna strata to suma zapłaconej premii netto. Strata ta występuje, gdy cena instrumentu bazowego równa się cenie wykonania opcji w momencie wygaśnięcia.
Spójrzmy jeszcze raz na sytuację Dark Poola, zakładając w uproszczeniu, że giełda kupiła 10 zleceń opcji sprzedaży 1 BTC po 40 000 USDT oraz 10 kupna po cenie 38 000 USDT. Za wszystkie złożone zlecenia Dark Pool wypłaca tokeny DPX, w ilościach wyznaczonych z modelu Blacka Scholesa. W przypadku ceny powyżej wartości 40 000 USDT, np. 42 000 USDT, realizowane jest 10 zleceń sprzedaży, klienci otrzymują za każdego BTC zgodnie z umową 40 000 USDT, a na każdym Dark Pool zarabia 2 000 USDT (sumarycznie 20 tys. USDT), 10 zleceń kupna nie zostaje zrealizowanych. W przypadku spadku ceny BTC poniżej 38 000 USDT, np. 36 000 USDT, opcje sprzedaży nie zostają zrealizowane, natomiast opcje kupna tak. A więc 10 zleceniodawców opcji kupna otrzymuje po 1 BTC i płaci za każdego Dark Poolowi 38 000 USDT, Dark Pool zarabia na każdym zleceniu różnice cen, a więc w sumie zarabia 20 tys. USDT. Zatem zarówno w przypadku wzrostu ceny ponad 40 000 USDT jak i spadku poniżej 38 000 USDT Dark Pool zarabia. W przypadku ceny poniżej 40 000, a powyżej 38 000 USDT, żadne ze zleceń nie zostaje zrealizowane. Wszystkim 20 klientom, niezależnie od ceny BTC, Dark Pool wypłaca premie w tokenach DPX. W przypadku wypłat premii poprzez własny token kluczowe znaczenie ma płynność oraz akceptacja tokenów przez rynek. Jeśli rynek zachowa się efektywnie, to wartość DPX będzie spadać w okresach niskiej zmienności oczekiwanej oraz rosnąć, gdy rynek będzie oczekiwał jej wzrostu.
––––––––––––––––––
1 Teoria gier została po raz pierwszy sformalizowana matematycznie w monografii Neumanna, i Morgensterna (J. v. Neumann i O. Morgenstern (1944) Theory of Games and Economic Behavior, Princeton Univ. Press.) Badania w zakresie teorii gier wielokrotnie zostały nagradzane przez komitet Nagrody Nobla: w 1978 Herbert Simon, w 1994 John Nash, Reinhard Selten i John Harsanyi, 1996 William Vickrey i James Mirrlees, 2005 Thomas C. Schelling i Robert J. Aumann 2007 Leonid Hurwicz, Eric S. Maskin, Roger B. Myerson.
2 Przy założeniu, że pojedynczy inwestor nie może poprzez swoje decyzje wpłynąć na ceny akcji.